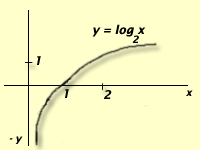
Se llama logaritmo de un número real positivo, b en base a otro número a también real positivo y diferente de 1, al número c que es el exponente a que hay que elevar la base a para obtener el número b
log a b = c si y solo si a c = b .
De acuerdo con la definición tenemos que:
Los números negativos no tienen logaritmo en el conjunto de los números reales .
Cuando la base de los logaritmos es mayor que 1, los números positivos menores que la unidad tienen logaritmo negativo:
log3 1/81 es igual a - 4 pues (3)- 4 = 1/81
Propiedades de los logaritmos
La logaritmación no es distributiva con respecto a la suma
log2( 2 + 4 + 8 + 2) log2 16 = 4 24 = 16
log22 = 1
log2 4 = 2
log2 8 = 3
log2 2 =1
7
No se cumple
No es distributiva con respecto a la resta
log2(64 - 32) log232 = 5 25
log264 = 6
log2 32 = 5
11
No se cumple
Tanto en la suma como en la resta se debe efectuar la operación y luego calcular el logaritmo.
Producto
El logaritmo de un producto en una base dada, es igual a la suma de los logaritmos de los factores en esa misma base.
loga( m . n) = logam + logan |
log5 (25 . 5) = log525 + log55 =log5 (25 . 5) = 2 + 1 = 3
log5125 = 3 pues53= 125
División
El logaritmo de un cociente en una base dada, es igual a la diferencia entre el logaritmo del dividendo y el del divisor.
loga( m : n) = logam - logan |
log2(64: 16) = log264 - log216 = 6 - 4 = 2
log2 4 = 2
Potencia
loga bn = n. log a b |
a) log2 8 4 = b) 4 . log 2 8
a) log2 4096 = 12 pues 212 = 4096
b) 4. 3 = 12
Radicación
loga√b = logab 2 |
a) log2 √16 b) log2 16
2
a) log2 4 = 2
b) 4 = 2
2
Logaritmo recíproco
loga 1 / b = - loga b |
log2 1 / 3 = -1 log2 3
Cambio de base
| loga b = log b / log a |
log2 16 = log 16 / log 2 = 1,2 / 0,301 = 3,98
Logaritmos naturales
El cambio de base expresa que todos los logaritmos pueden
ponerse en términos de uno solo.
Los logaritmos comunes
son los de base 10 y se designan como log
Los logaritmos de base e
que se llaman logaritmos naturales y se designan como ln .
log x = log 10 x , |
ln x = loge x . |
Función exponencial natural
La inversa de la función logaritmo natural ln x , se la denomina exponencial natural y sela designa como e x
a x = e x ln x
Inversa de la función logarítmica
1
1 + x
∫x 1 dt = In( 1 + x ) + C
1 + x
ex = lim ( 1 + x + x/ n)x log x = lim n ( x1/x - 1 )
x→∞ x→∞
Gráfica de la función logaritmo
Los gráficos de las funciones exponenciales cuando la base es mayor que 1 y cuando está entre 0 y 1.
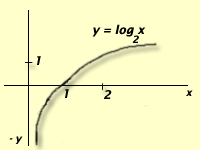
f ( x ) = log 2 x
La función f ( x ) = log a x es una función biyectiva de ]0, ∞[ en los reales.
Su función inversa que va de los reales en ]0,+ ∞ [ = función exponencial de base a = a x
la inversa de f ( x ) = log a x
f -1 : R → ]0,+ ∞[ x →a x
log 2 x
f -1 : R → ]0,+ ∞[ x →2 x
Escolared.com.ar - escolared@gmail.com