Derivadas
de funciones trigonométricas
A. Derivadas
de funciones trigonométricas básicas
|
|
|
|
|
|
|
|
|
Ejemplos para discusión:
Halla la derivada de:
1) y = 3
sen x
2) y = x
+ cos x
4) y = x
- tan x
5) y = x
sec x
Ejercicio
de práctica: Halla la derivada de:
1) y = 2 cos x
2) y = x2
- sen x
3) y = sec x
tan x
B. Derivadas
de funciones trigonométricas
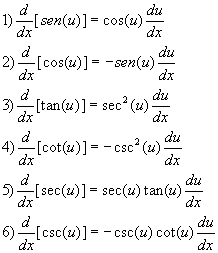
Ejemplos para
discusión: Halla la derivada de:
1) y =
sen 2x
2) y =
cos (x - 1)
3) y = x2
tan x2
4) y = tan3 4x
5) y = cos5 5x
6) Halla la derivada de y
respecto a x de sen y = x.
Ejercicio de
práctica: Halla la derivada de:
1) y = cos 3x2
2) y = sen (3x2
+ 5x - 7)
3) y = tan (2x2
+ 3)
Ejercicios:
Halla la derivada de cada una de las siguientes
funciones y evaluarlas en los casos indicados:
1) f(x) = sen x; 
2) f(x) = x2
– cos x; f’(½π)
3) y = 1 + 7 sen x – tan x
4) y = -10x
+ 3 cos x;
5) y = tan
x – x
6) y = 4
sen x – x; 
7) y = tan
x – csc x
8) y = x +
sen x
9) y = x
sen x
10) y = x2 sen x
11) y = x cos x
12) y = x5 cos x
13) y = x2
cos x
17) y = cos x3
18) f(x) = cos 3x; 
19) y = sen (2x2 + 3)
20) y = sen (πx + 1)
21) y = x2 sen 4x
22) y = 3 sen 2x
23) y = sen (3x2 + 5x – 7)
24) y = x3 cos x3
26) y = (1 – x2) sen x2
27) y = tan2 x
28) y = sen3 x
29) y = sen2 4x
30) y = csc2 2x
Respuestas:
|
|
|
|
2) f’(x) = 2x + sen
x; f’(½π) = π + 1 |
26) y’ = 2x(cos x2 – x2 cos x2 – sen x2) |
|
3) y’ = 7 cos x – sec2 x |
27) y’ = 2 tan x sec2 x |
|
|
28) y’ = 3 sen2 x cos x |
|
5) y’ = sec2 x – 1 |
29) y’ = 8 sen 4x cos 4x |
|
|
30) y’ = -4 csc2 2x cot 2x |
7) y’ =
sec2 x + csc x cot x
8) y’ = 1
+ cos x
9) y’ = x
cos x + sen x
10) y’ = x2 cos x + 2x sen x
11) y’ = cos x – x sen x
12) y’ = 5x4 cos x – x5 sen
x
13) y’ = -x2 sen x + 2x cos x
17) y’
= -3x2 sen x3
19) y’ = 4x cos (2x2 + 3)
20) y’ = π cos (πx + 1)
21) y’ = 2x sen 4x + 4x2 cos 4x
22) y’ = 6 cos 2x
23) y’ = (6x + 5) cos (3x2 + 5x – 7)
24) y’ = -3x5 sen x3 + 3x2
cos x3